| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 7 (Before Exercise 9.1) | Exercise 9.1 | |
Chapter 9 Some Applications Of Trigonometry
Welcome to the solutions guide for Chapter 9, "Some Applications of Trigonometry," commonly referred to as 'Heights and Distances,' from the latest Class 10 NCERT mathematics textbook for the academic session 2024-25. This chapter brilliantly showcases the practical power of trigonometry, demonstrating how the ratios learned in Chapter 8 can be applied to solve real-world problems involving the measurement of heights of objects (like towers, trees, buildings) and distances between points, often where direct measurement is impractical or impossible. These solutions are designed to provide clear, step-by-step guidance on translating word problems into geometric diagrams and applying trigonometric principles accurately.
The cornerstone of solving problems in this chapter lies in effective interpretation and visualization. The solutions emphasize the critical first step: carefully reading the problem statement and translating the scenario into a clear, labeled diagram. This typically involves representing the situation using points, lines, and, crucially, identifying the relevant right-angled triangle(s) within the diagram. Understanding key terminology is vital, and the solutions clarify and illustrate concepts such as:
- Line of Sight: The imaginary line drawn from the eye of an observer to the point on the object being viewed.
- Angle of Elevation: The angle formed by the line of sight with the horizontal when the object being viewed is above the horizontal level.
- Angle of Depression: The angle formed by the line of sight with the horizontal when the object being viewed is below the horizontal level. (Note: Due to parallel lines, the angle of depression from an observer to an object is equal to the angle of elevation from the object back to the observer).
Once the right-angled triangle(s) and the relevant angles are identified, the core technique involves selecting the appropriate trigonometric ratio (sine, cosine, or tangent) that connects the known side(s), the known angle, and the unknown side (height or distance) that needs to be calculated. The choice depends on whether the known/unknown sides are opposite, adjacent, or the hypotenuse relative to the given angle. The solutions demonstrate this selection process clearly, often utilizing the standard angle values learned in the previous chapter (primarily $30^\circ, 45^\circ, 60^\circ$, whose ratio values like $\sin 30^\circ = \frac{1}{2}$, $\tan 45^\circ = 1$, $\cos 60^\circ = \frac{1}{2}$, etc., are frequently required). An equation is then set up using the chosen ratio and solved algebraically to find the unknown quantity. Step-by-step calculations, including potential simplification or rationalization of denominators involving $\sqrt{3}$, are shown meticulously.
The solutions cover a diverse range of scenarios, progressively building complexity:
- Finding the height of a vertical object given an angle of elevation and distance from the base.
- Finding the distance to an object given its height and an angle of elevation or depression.
- Problems involving angles of elevation/depression from different points or to different points on the same object (e.g., top and bottom of a tower).
- Scenarios where the observer moves towards or away from the object, leading to a change in the angle of elevation, often requiring the use of two right triangles and solving a system of equations implicitly or explicitly.
Regarding the rationalized syllabus for 2024-25, Chapter 9, "Some Applications of Trigonometry," has been streamlined. Notably, exercises involving scenarios requiring the use of complementary angles explicitly (related to the removed section in Chapter 8) or problems featuring highly complex situations involving more than two triangles or intricate geometric setups have been removed or reduced. The focus is firmly on single-triangle problems and standard two-triangle problems involving angles of elevation and depression. By diligently working through these focused solutions, students can learn to effectively model real-world situations using diagrams, master the application of trigonometric ratios in practical contexts, and develop strong analytical and problem-solving skills for heights and distances calculations.
Example 1 to 7 (Before Exercise 9.1)
Example 1. A tower stands vertically on the ground. From a point on the ground, which is 15 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower.
Answer:
Given:
Let the tower be AB, standing vertically on the ground.
Let C be a point on the ground, 15 m away from the foot of the tower B.
Distance from the foot of the tower to the point, BC = $15\text{ m}$.
The angle of elevation of the top of the tower A from point C is $ \angle\text{ACB} = 60^\circ $.
To Find:
The height of the tower AB.
Construction Required:
Draw a vertical line segment AB representing the tower. Draw a horizontal line segment BC representing the distance on the ground from the foot of the tower to the observation point. Join A to C. $\triangle$ABC is a right-angled triangle at B. Label BC = 15 m and $\angle$ACB = 60$^\circ$.
Solution:
Consider the right-angled triangle ABC, where $\angle$B = $90^\circ$ (since the tower is vertical to the ground).
We need to find the height of the tower, AB.
We are given the length of the adjacent side BC (with respect to angle C) and the angle of elevation $\angle$C = $60^\circ$.
The trigonometric ratio that relates the opposite side (AB) and the adjacent side (BC) with respect to angle C is the tangent.
$\tan \text{C} = \frac{\text{Side opposite to angle C}}{\text{Side adjacent to angle C}} = \frac{\text{AB}}{\text{BC}}$
Substitute the given values:
$\tan 60^\circ = \frac{\text{AB}}{15}$
We know the standard value of $ \tan 60^\circ $, which is $ \sqrt{3} $.
So, the equation becomes:
$\sqrt{3} = \frac{\text{AB}}{15}$
To find the length of AB, multiply both sides of the equation by 15:
$ \text{AB} = 15 \times \sqrt{3} $
$ \text{AB} = 15\sqrt{3}\text{ m} $
Answer:
The height of the tower is $15\sqrt{3}\text{ m}$.
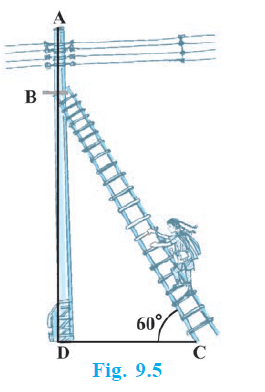
Example 2. An electrician has to repair an electric fault on a pole of height 5 m. She needs to reach a point 1.3m below the top of the pole to undertake the repair work (see Fig. 9.5). What should be the length of the ladder that she should use which, when inclined at an angle of 60° to the horizontal, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder? (You may take $\sqrt{3}$ = 1.73)
Answer:
Given:
Height of the pole = $5\text{ m}$.
The electrician needs to reach a point 1.3 m below the top of the pole.
Let the pole be represented by AB, where A is the top and B is the foot. AB = $5\text{ m}$.
Let C be the point on the pole where the electrician needs to reach. C is 1.3 m below A.
The distance BC = AB - 1.3 m = $5\text{ m} - 1.3\text{ m} = 3.7\text{ m}$.
Let the ladder be CD, placed with its foot at D on the ground and reaching point C on the pole.
The angle of inclination of the ladder with the horizontal ground is $60^\circ$. In the right-angled triangle CBD, where B is the foot of the pole and D is the foot of the ladder, $ \angle\text{B} = 90^\circ $, and $ \angle\text{CDB} = 60^\circ $.
The height the electrician needs to reach from the ground is BC = $3.7\text{ m}$.
To Find:
The length of the ladder CD.
The distance from the foot of the pole to the foot of the ladder, BD.
Solution:
Consider the right-angled triangle $\triangle$CBD.
We have BC = $3.7\text{ m}$ (side opposite to $60^\circ$) and $ \angle\text{CDB} = 60^\circ $.
To find the length of the ladder CD (the hypotenuse), we can use the sine ratio:
$\sin (\angle \text{CDB}) = \frac{\text{Opposite side}}{\text{Hypotenuse}} = \frac{\text{BC}}{\text{CD}}$
Substitute the values:
$\sin 60^\circ = \frac{3.7}{\text{CD}}$
We know that $ \sin 60^\circ = \frac{\sqrt{3}}{2} $.
So, the equation becomes:
$\frac{\sqrt{3}}{2} = \frac{3.7}{\text{CD}}$
Cross-multiply to solve for CD:
$ \text{CD} \times \sqrt{3} = 3.7 \times 2 $
$ \text{CD} \times \sqrt{3} = 7.4 $
$ \text{CD} = \frac{7.4}{\sqrt{3}} $
Using the value $ \sqrt{3} \approx 1.73 $:
$ \text{CD} \approx \frac{7.4}{1.73} $
$ \text{CD} \approx 4.27 \text{ m} $ (approximately)
To find the distance BD (the adjacent side), we can use the tangent ratio:
$\tan (\angle \text{CDB}) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{\text{BC}}{\text{BD}}$
Substitute the values:
$\tan 60^\circ = \frac{3.7}{\text{BD}}$
We know that $ \tan 60^\circ = \sqrt{3} $.
So, the equation becomes:
$\sqrt{3} = \frac{3.7}{\text{BD}}$
Solve for BD:
$ \text{BD} \times \sqrt{3} = 3.7 $
$ \text{BD} = \frac{3.7}{\sqrt{3}} $
Using the value $ \sqrt{3} \approx 1.73 $:
$ \text{BD} \approx \frac{3.7}{1.73} $
$ \text{BD} \approx 2.14 \text{ m} $ (approximately)
Thus, the length of the ladder should be approximately 4.27 m, and she should place the foot of the ladder approximately 2.14 m away from the foot of the pole.
Answer:
Length of the ladder $ \approx 4.27\text{ m} $.
Distance from the foot of the pole to the foot of the ladder $ \approx 2.14\text{ m} $.
Example 3. An observer 1.5 m tall is 28.5 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?
Answer:
Given:
Height of the observer = $1.5\text{ m}$.
Distance between the observer and the chimney = $28.5\text{ m}$.
Angle of elevation of the top of the chimney from the observer's eyes = $45^\circ$.
To Find:
The height of the chimney.
Construction Required:
Draw a vertical line segment AB representing the chimney. Draw a vertical line segment CD representing the observer, with C being the position of her eyes and D being her feet on the ground. Draw a horizontal line segment DB representing the distance between the observer and the chimney foot. Draw a horizontal line segment CE parallel to DB from C to AB, intersecting AB at E. $\triangle$AEC is a right-angled triangle at E. Label CD = 1.5 m, DB = 28.5 m, CE = DB, EB = CD, and $\angle$ACE = 45$^\circ$.
Solution:
Let the height of the chimney be AB.
Let the height of the observer be CD = $1.5\text{ m}$.
The distance between the observer and the chimney is BD = $28.5\text{ m}$.
Draw a line CE parallel to BD, such that C is the observer's eye level and E is a point on the chimney directly above the line of sight from C. Thus, CE = BD = $28.5\text{ m}$, and EB = CD = $1.5\text{ m}$.
The angle of elevation from the observer's eyes (C) to the top of the chimney (A) is $ \angle\text{ACE} = 45^\circ $.
Consider the right-angled triangle $\triangle$AEC. The right angle is at E.
We have CE = $28.5\text{ m}$ (adjacent side to $45^\circ$) and $ \angle\text{ACE} = 45^\circ $.
We need to find the length of AE (opposite side to $45^\circ$).
Using the tangent ratio in $\triangle$AEC:
$\tan (\angle \text{ACE}) = \frac{\text{Side opposite to angle ACE}}{\text{Side adjacent to angle ACE}} = \frac{\text{AE}}{\text{CE}}$
Substitute the values:
$\tan 45^\circ = \frac{\text{AE}}{28.5}$
We know that $ \tan 45^\circ = 1 $.
So, the equation becomes:
$1 = \frac{\text{AE}}{28.5}$
Multiply both sides by 28.5:
$ \text{AE} = 28.5 \times 1 $
$ \text{AE} = 28.5\text{ m} $
The total height of the chimney AB is the sum of AE and EB.
$ \text{AB} = \text{AE} + \text{EB} $
Since EB is equal to the height of the observer CD, EB = $1.5\text{ m}$.
$ \text{AB} = 28.5\text{ m} + 1.5\text{ m} $
$ \text{AB} = 30\text{ m} $
Answer:
The height of the chimney is $30\text{ m}$.
Example 4. From a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45°. Find the length of the flagstaff and the distance of the building from the point P. (You may take $\sqrt{3}$ = 1.732)
Answer:
Given:
Let the height of the building be AB = $10\text{ m}$.
A flagstaff is hoisted at the top of the building. Let the flagstaff be represented by AC, where A is the top of the building and C is the top of the flagstaff. So the total height from the ground to the top of the flagstaff is BC = BA + AC = $10\text{ m} + \text{AC}$.
Let P be a point on the ground.
The angle of elevation of the top of the building (A) from point P is $ \angle\text{BPA} = 30^\circ $. (Assuming B is the foot of the building).
The angle of elevation of the top of the flagstaff (C) from point P is $ \angle\text{BPC} = 45^\circ $. (Assuming B is the foot of the building).
The building is vertical to the ground, so $ \angle\text{PBA} = 90^\circ $.
To Find:
The length of the flagstaff AC.
The distance of the building from point P, PB.
Construction Required:
Draw a vertical line segment BD representing the building (AB=10m) with flagstaff (AC) on top, where D is the foot of the building. Let P be a point on the ground. Draw a horizontal line segment PD. Join PA and PC. $\triangle$PBD and $\triangle$PCD are right-angled triangles at D. $\angle$APD = 30$^\circ$ and $\angle$CPD = 45$^\circ$. (Let's adjust variables to match standard notation). Let the building be AB (A top, B foot, AB=10m). Flagstaff AC on top of A. C is the top of flagstaff. P is the ground point. $\angle$APB = 30$^\circ$, $\angle$CPB = 45$^\circ$. $\triangle$PBA and $\triangle$PBC are right-angled at B. Let's use this representation.
Draw a vertical line segment AB representing the building (AB=10m). Draw a vertical line segment AC representing the flagstaff on top of the building. C is the top of the flagstaff. B is the foot of the building. Let P be a point on the ground. Draw a horizontal line segment PB. Join PA and PC. $\triangle$PBA and $\triangle$PBC are right-angled triangles at B. $\angle$APB = 30$^\circ$ and $\angle$CPB = 45$^\circ$.
Solution:
Let the height of the building be AB = $10\text{ m}$.
Let the length of the flagstaff be $h$. The flagstaff is on top of the building, so the total height from the ground to the top of the flagstaff is BC = AB + AC. Let AC = $h\text{ m}$. So, BC = $10 + h$ meters.
Let P be the point on the ground, and let PB be the distance from the foot of the building to point P. We assume the building is vertical, so $\angle$PBA = $90^\circ$.
The angle of elevation of the top of the building (A) from P is $ \angle\text{APB} = 30^\circ $.
The angle of elevation of the top of the flagstaff (C) from P is $ \angle\text{CPB} = 45^\circ $.
Consider the right-angled triangle $\triangle$PBA.
We have the opposite side AB = $10\text{ m}$ (with respect to angle 30$^\circ$) and we want to find the adjacent side PB.
Using the tangent ratio in $\triangle$PBA:
$\tan (\angle \text{APB}) = \frac{\text{Side opposite to angle APB}}{\text{Side adjacent to angle APB}} = \frac{\text{AB}}{\text{PB}}$
Substitute the values:
$\tan 30^\circ = \frac{10}{\text{PB}}$
We know that $ \tan 30^\circ = \frac{1}{\sqrt{3}} $.
So, the equation is:
$\frac{1}{\sqrt{3}} = \frac{10}{\text{PB}}$
Cross-multiply to solve for PB:
$ \text{PB} = 10 \times \sqrt{3} $
$ \text{PB} = 10\sqrt{3}\text{ m} $
Using the value $ \sqrt{3} \approx 1.732 $:
$ \text{PB} = 10 \times 1.732 = 17.32\text{ m} $
The distance of the building from point P is $10\sqrt{3}\text{ m}$ or approximately $17.32\text{ m}$.
Now, consider the right-angled triangle $\triangle$PBC.
We have the opposite side BC = $10 + h$ and the adjacent side PB = $10\sqrt{3}\text{ m}$. The angle of elevation is $ \angle\text{CPB} = 45^\circ $.
Using the tangent ratio in $\triangle$PBC:
$\tan (\angle \text{CPB}) = \frac{\text{Side opposite to angle CPB}}{\text{Side adjacent to angle CPB}} = \frac{\text{BC}}{\text{PB}}$
Substitute the values:
$\tan 45^\circ = \frac{10 + h}{10\sqrt{3}}$
We know that $ \tan 45^\circ = 1 $.
So, the equation is:
$1 = \frac{10 + h}{10\sqrt{3}}$
Multiply both sides by $ 10\sqrt{3} $:
$ 10\sqrt{3} = 10 + h $
Solve for $ h $ (the length of the flagstaff AC):
$ h = 10\sqrt{3} - 10 $
$ h = 10 (\sqrt{3} - 1)\text{ m} $
Using the value $ \sqrt{3} \approx 1.732 $:
$ h = 10 (1.732 - 1) $
$ h = 10 (0.732) $
$ h = 7.32\text{ m} $
Answer:
The length of the flagstaff is $10(\sqrt{3} - 1)\text{ m}$ or approximately $7.32\text{ m}$.
The distance of the building from point P is $10\sqrt{3}\text{ m}$ or approximately $17.32\text{ m}$.
Example 5. The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.
Answer:
Given:
Let the height of the tower be AB = $h\text{ m}$.
Let B be the foot of the tower.
Let C be the point on the ground where the shadow ends when the Sun's altitude (angle of elevation of the top of the tower) is $60^\circ$. So, $ \angle\text{ACB} = 60^\circ $. Let BC = $x\text{ m}$.
Let D be the point on the ground where the shadow ends when the Sun's altitude is $30^\circ$. So, $ \angle\text{ADB} = 30^\circ $. Point C lies between B and D.
The shadow is 40 m longer at $30^\circ$ than at $60^\circ$. This means the difference in the lengths of the shadows is 40 m. So, BD - BC = 40 m, which means CD = $40\text{ m}$.
The tower is vertical, so $ \angle\text{ABC} = \angle\text{ABD} = 90^\circ $.
To Find:
The height of the tower AB = $h$.
Construction Required:
Draw a vertical line segment AB representing the tower. Draw a horizontal line segment BD on the ground. Mark point C on BD such that BC is the length of the shadow when the angle of elevation from C to A is 60$^\circ$. Mark point D such that BD is the length of the shadow when the angle of elevation from D to A is 30$^\circ$. C should be between B and D. Label CD = 40m. Draw lines AC and AD. $\triangle$ABC and $\triangle$ABD are right-angled at B. Label $\angle$ACB = 60$^\circ$ and $\angle$ADB = 30$^\circ$.
Solution:
Consider the right-angled triangle $\triangle$ABC.
We have the opposite side AB = $h$ and the adjacent side BC = $x$. The angle of elevation from C is $60^\circ$.
Using the tangent ratio in $\triangle$ABC:
$\tan (\angle \text{ACB}) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{\text{AB}}{\text{BC}}$
Substitute the values:
$\tan 60^\circ = \frac{h}{x}$
We know that $ \tan 60^\circ = \sqrt{3} $.
So, the equation is:
$\sqrt{3} = \frac{h}{x}$
From this, we can express $x$ in terms of $h$:
$x = \frac{h}{\sqrt{3}}$
... (i)
Now, consider the right-angled triangle $\triangle$ABD.
We have the opposite side AB = $h$ and the adjacent side BD = BC + CD = $x + 40$. The angle of elevation from D is $30^\circ$.
Using the tangent ratio in $\triangle$ABD:
$\tan (\angle \text{ADB}) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{\text{AB}}{\text{BD}}$
Substitute the values:
$\tan 30^\circ = \frac{h}{x + 40}$
We know that $ \tan 30^\circ = \frac{1}{\sqrt{3}} $.
So, the equation is:
$\frac{1}{\sqrt{3}} = \frac{h}{x + 40}$
Cross-multiply:
$x + 40 = h\sqrt{3}$
Now, substitute the expression for $x$ from equation (i) into this equation:
$\frac{h}{\sqrt{3}} + 40 = h\sqrt{3}$
To solve for $h$, move the term $ \frac{h}{\sqrt{3}} $ to the right side of the equation:
$ 40 = h\sqrt{3} - \frac{h}{\sqrt{3}} $
Factor out $h$ from the terms on the right side:
$ 40 = h \left(\sqrt{3} - \frac{1}{\sqrt{3}}\right) $
Find a common denominator inside the parenthesis:
$ 40 = h \left(\frac{\sqrt{3} \times \sqrt{3}}{\sqrt{3}} - \frac{1}{\sqrt{3}}\right) $
$ 40 = h \left(\frac{3}{\sqrt{3}} - \frac{1}{\sqrt{3}}\right) $
$ 40 = h \left(\frac{3 - 1}{\sqrt{3}}\right) $
$ 40 = h \left(\frac{2}{\sqrt{3}}\right) $
To isolate $h$, multiply both sides by $ \frac{\sqrt{3}}{2} $:
$ h = 40 \times \frac{\sqrt{3}}{2} $
$ h = \frac{40}{2} \times \sqrt{3} $
$ h = 20\sqrt{3} $
Answer:
The height of the tower is $20\sqrt{3}\text{ m}$.
Example 6. The angles of depression of the top and the bottom of an 8 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building and the distance between the two buildings.
Answer:
Given:
Let the multi-storeyed building be represented by AB, where A is the top and B is the foot.
Let the 8 m tall building be represented by CD, where C is the top and D is the foot. CD = $8\text{ m}$.
Let the distance between the two buildings be BD. Draw a horizontal line CE from C to AB, such that E is on AB. Then CBDE is a rectangle, so CE = BD and EB = CD = $8\text{ m}$.
The height of the multi-storeyed building is AB = AE + EB = AE + $8\text{ m}$.
Let PX be a horizontal line from the top of the multi-storeyed building A. The angles of depression from A are measured from this horizontal line.
The angle of depression of the top of the 8 m building (C) from A is $30^\circ$. So, $ \angle\text{XAC} = 30^\circ $. Since PX is horizontal and CE is horizontal, PX || CE. The alternate interior angle $ \angle\text{ACE} = \angle\text{XAC} = 30^\circ $. Triangle AEC is right-angled at E.
The angle of depression of the bottom of the 8 m building (D) from A is $45^\circ$. So, $ \angle\text{XAD} = 45^\circ $. Since PX is horizontal and BD is horizontal, PX || BD. The alternate interior angle $ \angle\text{ADB} = \angle\text{XAD} = 45^\circ $. Triangle ABD is right-angled at B.
To Find:
The height of the multi-storeyed building (AB) and the distance between the two buildings (BD).
Construction Required:
Draw two vertical lines representing the buildings. Label the multi-storeyed building AB (A top, B foot) and the shorter building CD (C top, D foot, CD=8m). Draw a horizontal line BD between their bases. Draw a horizontal line CE from C to AB, meeting AB at E. Draw a horizontal line AX from the top of the multi-storeyed building A. Label angles of depression $\angle$XAC=30$^\circ$ and $\angle$XAD=45$^\circ$. Use alternate interior angles $\angle$ACE=30$^\circ$ and $\angle$ADB=45$^\circ$. $\triangle$AEC and $\triangle$ABD are right-angled at E and B respectively. Label EB = CD = 8m and CE = BD.
Solution:
Let the height of the multi-storeyed building be AB = $H\text{ m}$.
Let the distance between the two buildings be BD = $D\text{ m}$.
We have a rectangle CBDE, so CE = BD = $D\text{ m}$ and EB = CD = $8\text{ m}$.
The part of the multi-storeyed building above C is AE = AB - EB = $H - 8\text{ m}$.
Consider the right-angled triangle $\triangle$ABD.
We have the opposite side AB = $H$ and the adjacent side BD = $D$. The angle of elevation from D to A is $ \angle\text{ADB} = 45^\circ $.
Using the tangent ratio in $\triangle$ABD:
$\tan (\angle \text{ADB}) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{\text{AB}}{\text{BD}}$
Substitute the values:
$\tan 45^\circ = \frac{H}{D}$
We know that $ \tan 45^\circ = 1 $.
So, the equation is:
$1 = \frac{H}{D}$
Multiply both sides by D:
$H = D$
... (i)
Now, consider the right-angled triangle $\triangle$AEC.
We have the opposite side AE = $H - 8$ and the adjacent side CE = $D$. The angle $\angle$ACE = $30^\circ$.
Using the tangent ratio in $\triangle$AEC:
$\tan (\angle \text{ACE}) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{\text{AE}}{\text{CE}}$
Substitute the values:
$\tan 30^\circ = \frac{H - 8}{D}$
We know that $ \tan 30^\circ = \frac{1}{\sqrt{3}} $.
So, the equation is:
$\frac{1}{\sqrt{3}} = \frac{H - 8}{D}$
... (ii)
Substitute $ D = H $ from equation (i) into equation (ii):
$\frac{1}{\sqrt{3}} = \frac{H - 8}{H}$
Cross-multiply:
$ 1 \times H = \sqrt{3} \times (H - 8) $
$ H = \sqrt{3}H - 8\sqrt{3} $
Rearrange the terms to solve for H. Move the $ \sqrt{3}H $ term to the left side or the H term to the right side:
$ 8\sqrt{3} = \sqrt{3}H - H $
Factor out H from the terms on the right side:
$ 8\sqrt{3} = H(\sqrt{3} - 1) $
Divide by $ (\sqrt{3} - 1) $ to find H:
$ H = \frac{8\sqrt{3}}{\sqrt{3} - 1} $
To simplify the expression and remove the radical from the denominator, we rationalize the denominator by multiplying the numerator and the denominator by the conjugate of $ \sqrt{3} - 1 $, which is $ \sqrt{3} + 1 $.
$ H = \frac{8\sqrt{3}}{(\sqrt{3} - 1)} \times \frac{(\sqrt{3} + 1)}{(\sqrt{3} + 1)} $
Using the identity $ (a-b)(a+b) = a^2 - b^2 $ in the denominator:
$ H = \frac{8\sqrt{3}(\sqrt{3} + 1)}{(\sqrt{3})^2 - (1)^2} $
$ H = \frac{(8\sqrt{3} \times \sqrt{3}) + (8\sqrt{3} \times 1)}{3 - 1} $
$ H = \frac{(8 \times 3) + 8\sqrt{3}}{2} $
$ H = \frac{24 + 8\sqrt{3}}{2} $
Divide both terms in the numerator by 2:
$ H = \frac{24}{2} + \frac{8\sqrt{3}}{2} $
$ H = 12 + 4\sqrt{3}\text{ m} $
Since $ D = H $ (from equation i):
$ D = 12 + 4\sqrt{3}\text{ m} $
Answer:
The height of the multi-storeyed building is $ (12 + 4\sqrt{3})\text{ m} $.
The distance between the two buildings is $ (12 + 4\sqrt{3})\text{ m} $.
Example 7. From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°, respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.
Answer:
Given:
A point P on a bridge across a river.
The height of the bridge from the banks is $3\text{ m}$. Let PM be the perpendicular distance from the point P on the bridge to the river surface (or the level of the banks), where M is a point directly below P. PM = $3\text{ m}$.
Let the banks of the river on opposite sides be at points A and B, such that M lies on the line segment AB. The width of the river is AB = AM + MB.
The angles of depression from P to the banks A and B are $30^\circ$ and $45^\circ$. Let PX be a horizontal line from P. $\angle$XPA = $30^\circ$ and $\angle$XPB = $45^\circ$.
Since PX is a horizontal line and AB represents the level of the banks (horizontal), PX is parallel to AB.
Therefore, the alternate interior angles are equal: $ \angle\text{PAM} = \angle\text{XPA} = 30^\circ $ and $ \angle\text{PBM} = \angle\text{XPB} = 45^\circ $.
PM is perpendicular to the river banks, so $ \angle\text{PMA} = 90^\circ $ and $ \angle\text{PMB} = 90^\circ $. Thus, $\triangle$PMA and $\triangle$PMB are right-angled triangles at M.
To Find:
The width of the river AB.
Construction Required:
Draw a horizontal line segment representing the river banks AB. Mark a point M on AB. Draw a vertical line segment MP representing the height of the bridge above the banks, with P being the point on the bridge. MP = 3m. Draw lines PA and PB. Draw a horizontal line PX through P. Label angles of depression $\angle$XPA=30$^\circ$ and $\angle$XPB=45$^\circ$. Use alternate interior angles $\angle$PAM=30$^\circ$ and $\angle$PBM=45$^\circ$. $\triangle$PMA and $\triangle$PMB are right-angled at M.
Solution:
Let the height of the bridge from the banks be PM = $3\text{ m}$.
Let the width of the river be AB = AM + MB.
Consider the right-angled triangle $\triangle$PMA.
We have the opposite side PM = $3\text{ m}$ (with respect to angle $30^\circ$) and we want to find the adjacent side AM.
Using the tangent ratio in $\triangle$PMA:
$\tan (\angle \text{PAM}) = \frac{\text{Side opposite to angle PAM}}{\text{Side adjacent to angle PAM}} = \frac{\text{PM}}{\text{AM}}$
Substitute the values:
$\tan 30^\circ = \frac{3}{\text{AM}}$
We know that $ \tan 30^\circ = \frac{1}{\sqrt{3}} $.
So, the equation is:
$\frac{1}{\sqrt{3}} = \frac{3}{\text{AM}}$
Cross-multiply to solve for AM:
$ \text{AM} = 3 \times \sqrt{3} $
$ \text{AM} = 3\sqrt{3}\text{ m} $
Now, consider the right-angled triangle $\triangle$PMB.
We have the opposite side PM = $3\text{ m}$ (with respect to angle $45^\circ$) and we want to find the adjacent side MB.
Using the tangent ratio in $\triangle$PMB:
$\tan (\angle \text{PBM}) = \frac{\text{Side opposite to angle PBM}}{\text{Side adjacent to angle PBM}} = \frac{\text{PM}}{\text{MB}}$
Substitute the values:
$\tan 45^\circ = \frac{3}{\text{MB}}$
We know that $ \tan 45^\circ = 1 $.
So, the equation is:
$1 = \frac{3}{\text{MB}}$
Cross-multiply to solve for MB:
$ \text{MB} = 3 \times 1 $
$ \text{MB} = 3\text{ m} $
The width of the river is the sum of AM and MB.
$ \text{AB} = \text{AM} + \text{MB} $
$ \text{AB} = 3\sqrt{3}\text{ m} + 3\text{ m} $
$ \text{AB} = 3(\sqrt{3} + 1)\text{ m} $
Answer:
The width of the river is $3(\sqrt{3} + 1)\text{ m}$.
Exercise 9.1
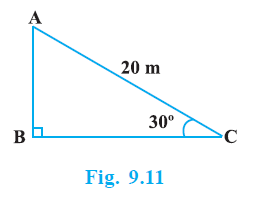
Question 1. A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see Fig. 9.11).
Answer:
Given:
Let AB be the vertical pole and AC be the rope. C is the point on the ground where the rope is tied.
Length of the rope, AC = 20 m.
Angle made by the rope with the ground, $\angle$ACB = 30$^\circ$.
The pole is vertical to the ground, so $\angle$ABC = 90$^\circ$.
To Find:
The height of the pole, AB.
Solution:
Consider the right-angled triangle $\triangle$ABC.
We need to find the side AB (opposite to the angle $\angle$C) and we are given the hypotenuse AC.
We can use the sine trigonometric ratio:
$\sin (\angle ACB) = \frac{\text{Opposite side}}{\text{Hypotenuse}}$
$\sin 30^\circ = \frac{AB}{AC}$
Substitute the given values:
$\sin 30^\circ = \frac{AB}{20}$
... (i)
We know that the value of $\sin 30^\circ$ is $\frac{1}{2}$.
Substitute this value into equation (i):
$\frac{1}{2} = \frac{AB}{20}$
Now, we solve for AB by cross-multiplication:
$2 \times AB = 1 \times 20$
$2AB = 20$
$AB = \frac{20}{2}$
$AB = 10$
... (ii)
Thus, the height of the pole is 10 meters.
Question 2. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Answer:
Given:
Let the tree be initially AB, broken at C, and the top A touches the ground at D. So, the standing part is BC and the broken part is AC, where AC = CD.
The distance from the foot of the tree (B) to the point where the top touches the ground (D) is BD = 8 m.
The angle made by the broken part with the ground is $\angle$CDB = 30$^\circ$.
The tree was vertical, so $\angle$CBD = 90$^\circ$.
The original height of the tree is AB = BC + AC = BC + CD.
To Find:
The height of the tree, AB.
Solution:
Consider the right-angled triangle $\triangle$CBD.
We need to find BC (opposite side) and CD (hypotenuse), given BD (adjacent side) and $\angle$D = 30$^\circ$.
To find BC, use the tangent ratio:
$\tan (\angle CDB) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 30^\circ = \frac{BC}{BD}$
Substitute the given values:
$\tan 30^\circ = \frac{BC}{8}$
... (i)
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
Substitute this value into equation (i):
$\frac{1}{\sqrt{3}} = \frac{BC}{8}$
Solve for BC:
$BC = \frac{8}{\sqrt{3}}$ m
... (ii)
To find CD, use the cosine ratio:
$\cos (\angle CDB) = \frac{\text{Adjacent side}}{\text{Hypotenuse}}$
$\cos 30^\circ = \frac{BD}{CD}$
Substitute the given values:
$\cos 30^\circ = \frac{8}{CD}$
... (iii)
We know that $\cos 30^\circ = \frac{\sqrt{3}}{2}$.
Substitute this value into equation (iii):
$\frac{\sqrt{3}}{2} = \frac{8}{CD}$
Solve for CD by cross-multiplication:
$CD \times \sqrt{3} = 8 \times 2$
$CD = \frac{16}{\sqrt{3}}$ m
... (iv)
The original height of the tree is AB = BC + AC. Since AC = CD (from the problem statement), we have AB = BC + CD.
Add the values of BC and CD from equations (ii) and (iv):
$AB = \frac{8}{\sqrt{3}} + \frac{16}{\sqrt{3}}$
$AB = \frac{8 + 16}{\sqrt{3}}$
$AB = \frac{24}{\sqrt{3}}$
Rationalize the denominator:
$AB = \frac{24}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
$AB = \frac{24\sqrt{3}}{3}$
$AB = 8\sqrt{3}$ m
... (v)
Thus, the height of the tree is $8\sqrt{3}$ meters.
Question 3. A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Answer:
We will solve this problem for the two cases separately.
Case 1: For children below 5 years
Given:
Let the height of the slide be AB = 1.5 m.
The angle of inclination with the ground is $\angle$ACB = 30$^\circ$.
$\triangle$ABC is a right-angled triangle at B ($\angle$ABC = 90$^\circ$).
To Find:
The length of the slide, AC.
Solution:
Consider the right-angled triangle $\triangle$ABC.
We need to find the hypotenuse AC, given the opposite side AB and the angle $\angle$C.
Use the sine ratio:
$\sin (\angle ACB) = \frac{\text{Opposite side}}{\text{Hypotenuse}}$
$\sin 30^\circ = \frac{AB}{AC}$
Substitute the given values:
$\sin 30^\circ = \frac{1.5}{AC}$
... (i)
We know that $\sin 30^\circ = \frac{1}{2}$.
Substitute this value into equation (i):
$\frac{1}{2} = \frac{1.5}{AC}$
Solve for AC by cross-multiplication:
$1 \times AC = 1.5 \times 2$
$AC = 3$ m
... (ii)
The length of the slide for children below 5 years is 3 meters.
Case 2: For elder children
Given:
Let the height of the slide be PQ = 3 m.
The angle of inclination with the ground is $\angle$PRQ = 60$^\circ$.
$\triangle$PQR is a right-angled triangle at Q ($\angle$PQR = 90$^\circ$).
To Find:
The length of the slide, PR.
Solution:
Consider the right-angled triangle $\triangle$PQR.
We need to find the hypotenuse PR, given the opposite side PQ and the angle $\angle$R.
Use the sine ratio:
$\sin (\angle PRQ) = \frac{\text{Opposite side}}{\text{Hypotenuse}}$
$\sin 60^\circ = \frac{PQ}{PR}$
Substitute the given values:
$\sin 60^\circ = \frac{3}{PR}$
... (iii)
We know that $\sin 60^\circ = \frac{\sqrt{3}}{2}$.
Substitute this value into equation (iii):
$\frac{\sqrt{3}}{2} = \frac{3}{PR}$
Solve for PR by cross-multiplication:
$PR \times \sqrt{3} = 3 \times 2$
$PR = \frac{6}{\sqrt{3}}$
Rationalize the denominator:
$PR = \frac{6}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
$PR = \frac{6\sqrt{3}}{3}$
$PR = 2\sqrt{3}$ m
... (iv)
The length of the slide for elder children is $2\sqrt{3}$ meters.
Question 4. The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Answer:
Given:
Let AB be the tower, where A is the top and B is the foot on the ground.
Let C be a point on the ground 30 m away from the foot of the tower B.
Distance from the foot of the tower to the point, BC = 30 m.
The angle of elevation of the top of the tower A from point C is $\angle$ACB = 30$^\circ$.
The tower is vertical to the ground, so $\angle$ABC = 90$^\circ$.
To Find:
The height of the tower, AB.
Solution:
Consider the right-angled triangle $\triangle$ABC.
We need to find the side AB (opposite to the angle $\angle$C) and we are given the adjacent side BC.
We can use the tangent trigonometric ratio:
$\tan (\angle ACB) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 30^\circ = \frac{AB}{BC}$
Substitute the given values:
$\tan 30^\circ = \frac{AB}{30}$
... (i)
We know that $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
Substitute this value into equation (i):
$\frac{1}{\sqrt{3}} = \frac{AB}{30}$
Solve for AB by cross-multiplication:
$AB \times \sqrt{3} = 30 \times 1$
$AB = \frac{30}{\sqrt{3}}$
Rationalize the denominator:
$AB = \frac{30}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
$AB = \frac{30\sqrt{3}}{3}$
$AB = 10\sqrt{3}$ m
... (ii)
Thus, the height of the tower is $10\sqrt{3}$ meters.
Question 5. A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Answer:
Given:
Let A be the position of the kite and B be the point on the ground directly below the kite. Let C be the point on the ground where the string is tied.
Height of the kite above the ground, AB = 60 m.
The string is AC.
The inclination of the string with the ground is $\angle$ACB = 60$^\circ$.
The height is vertical to the ground, so $\angle$ABC = 90$^\circ$.
We assume the string is tightly stretched (no slack).
To Find:
The length of the string, AC.
Solution:
Consider the right-angled triangle $\triangle$ABC.
We need to find the hypotenuse AC, given the opposite side AB and the angle $\angle$C.
Use the sine ratio:
$\sin (\angle ACB) = \frac{\text{Opposite side}}{\text{Hypotenuse}}$
$\sin 60^\circ = \frac{AB}{AC}$
Substitute the given values:
$\sin 60^\circ = \frac{60}{AC}$
... (i)
We know that $\sin 60^\circ = \frac{\sqrt{3}}{2}$.
Substitute this value into equation (i):
$\frac{\sqrt{3}}{2} = \frac{60}{AC}$
Solve for AC by cross-multiplication:
$AC \times \sqrt{3} = 60 \times 2$
$AC = \frac{120}{\sqrt{3}}$
Rationalize the denominator:
$AC = \frac{120}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
$AC = \frac{120\sqrt{3}}{3}$
$AC = 40\sqrt{3}$ m
... (ii)
Thus, the length of the string is $40\sqrt{3}$ meters.
Question 6. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Answer:
Given:
Let the height of the building be AB = 30 m.
Height of the boy = 1.5 m.
Let the boy's initial position be at C on the ground, and his eyes be at P. Draw PE parallel to the ground, such that E is on AB. Then BE = 1.5 m.
The height of the building above the boy's eye level is AE = AB - BE = 30 m - 1.5 m = 28.5 m.
The initial angle of elevation from P to the top of the building A is $\angle$APE = 30$^\circ$.
The boy walks towards the building to a new position D on the ground, and his eyes are at R. Draw RF parallel to the ground, such that F is on AB. Then BF = 1.5 m.
The height of the building above the boy's eye level is AF = AB - BF = 30 m - 1.5 m = 28.5 m. (Note: E and F are the same point on the line AB, let's call it E).
Let the initial distance from the boy's eye level to the building be PE. Let the final distance be RE.
The initial angle of elevation from R to A is $\angle$ARE = 60$^\circ$.
The distance the boy walked is CD = PR.
To Find:
The distance the boy walked, CD (or PR).
Solution:
Consider the right-angled triangle $\triangle$APE.
We have AE = 28.5 m and $\angle$APE = 30$^\circ$. We need to find PE.
Using the tangent ratio in $\triangle$APE:
$\tan (\angle APE) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{AE}{PE}$
Substitute the values:
$\tan 30^\circ = \frac{28.5}{PE}$
... (i)
We know $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
$\frac{1}{\sqrt{3}} = \frac{28.5}{PE}$
Solving for PE:
$PE = 28.5\sqrt{3}$ m
... (ii)
Now, consider the right-angled triangle $\triangle$ARE.
We have AE = 28.5 m and $\angle$ARE = 60$^\circ$. We need to find RE.
Using the tangent ratio in $\triangle$ARE:
$\tan (\angle ARE) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{AE}{RE}$
Substitute the values:
$\tan 60^\circ = \frac{28.5}{RE}$
... (iii)
We know $\tan 60^\circ = \sqrt{3}$.
$\sqrt{3} = \frac{28.5}{RE}$
Solving for RE:
$RE = \frac{28.5}{\sqrt{3}}$ m
... (iv)
The distance the boy walked towards the building is the difference between his initial distance (PE) and final distance (RE) from the line passing through E.
Distance walked = PE - RE
Substitute the values from equations (ii) and (iv):
Distance walked $= 28.5\sqrt{3} - \frac{28.5}{\sqrt{3}}$
Take 28.5 common:
Distance walked $= 28.5 \left(\sqrt{3} - \frac{1}{\sqrt{3}}\right)$
Combine the terms inside the bracket:
Distance walked $= 28.5 \left(\frac{(\sqrt{3})^2 - 1}{\sqrt{3}}\right)$
Distance walked $= 28.5 \left(\frac{3 - 1}{\sqrt{3}}\right)$
Distance walked $= 28.5 \left(\frac{2}{\sqrt{3}}\right)$
Distance walked $= \frac{57}{\sqrt{3}}$
Rationalize the denominator:
Distance walked $= \frac{57}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
Distance walked $= \frac{57\sqrt{3}}{3}$
Distance walked $= 19\sqrt{3}$ m
... (v)
Thus, the distance the boy walked towards the building is $19\sqrt{3}$ meters.
Question 7. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Answer:
Given:
Let AB be the building, with height AB = 20 m.
Let AC be the transmission tower fixed at the top of the building, where C is the top of the tower and A is the bottom of the tower (which is the top of the building).
Let P be a point on the ground.
The angle of elevation of the bottom of the tower (A) from P is $\angle$APB = 45$^\circ$.
The angle of elevation of the top of the tower (C) from P is $\angle$CPB = 60$^\circ$.
The building is vertical to the ground, so $\angle$PBA = 90$^\circ$.
Let the height of the tower be AC = $h$ m.
The total height from the ground to the top of the tower is BC = AB + AC = 20 + $h$ m.
Let the distance from point P to the foot of the building B be PB = $x$ m.
To Find:
The height of the transmission tower, $h$ (AC).
Solution:
Consider the right-angled triangle $\triangle$PBA.
In $\triangle$PBA, we have AB = 20 m, PB = $x$, and $\angle$APB = 45$^\circ$.
Using the tangent ratio:
$\tan (\angle APB) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{AB}{PB}$
Substitute the values:
$\tan 45^\circ = \frac{20}{x}$
... (i)
We know $\tan 45^\circ = 1$.
$1 = \frac{20}{x}$
Solving for $x$:
$x = 20$ m
... (ii)
Now, consider the right-angled triangle $\triangle$PBC.
In $\triangle$PBC, we have BC = $20 + h$, PB = $x$, and $\angle$CPB = 60$^\circ$.
Using the tangent ratio:
$\tan (\angle CPB) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{BC}{PB}$
Substitute the values:
$\tan 60^\circ = \frac{20 + h}{x}$
... (iii)
We know $\tan 60^\circ = \sqrt{3}$. Also, substitute $x=20$ from equation (ii) into equation (iii):
$\sqrt{3} = \frac{20 + h}{20}$
Multiply both sides by 20:
$20\sqrt{3} = 20 + h$
Solve for $h$:
$h = 20\sqrt{3} - 20$
Factor out 20:
$h = 20(\sqrt{3} - 1)$ m
... (iv)
Thus, the height of the transmission tower is $20(\sqrt{3} - 1)$ meters.
Question 8. A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Answer:
Given:
Let the pedestal be AB, where A is the top and B is the foot on the ground.
Let the statue be AC, standing on the top of the pedestal, where C is the top of the statue and A is the bottom of the statue (which is the top of the pedestal).
Height of the statue, AC = 1.6 m.
Let the height of the pedestal be AB = $h$ m.
The total height from the ground to the top of the statue is BC = AB + AC = $h + 1.6$ m.
Let P be a point on the ground.
Let the distance from point P to the foot of the pedestal B be PB = $x$ m.
The angle of elevation of the top of the pedestal (A) from P is $\angle$APB = 45$^\circ$.
The angle of elevation of the top of the statue (C) from P is $\angle$CPB = 60$^\circ$.
The pedestal is vertical to the ground, so $\angle$PBA = 90$^\circ$.
To Find:
The height of the pedestal, $h$ (AB).
Solution:
Consider the right-angled triangle $\triangle$PBA.
In $\triangle$PBA, we have AB = $h$, PB = $x$, and $\angle$APB = 45$^\circ$.
Using the tangent ratio:
$\tan (\angle APB) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{AB}{PB}$
Substitute the values:
$\tan 45^\circ = \frac{h}{x}$
... (i)
We know $\tan 45^\circ = 1$.
$1 = \frac{h}{x}$
Solving for $x$:
$x = h$ m
... (ii)
Now, consider the right-angled triangle $\triangle$PCB.
In $\triangle$PCB, we have BC = $h + 1.6$, PB = $x$, and $\angle$CPB = 60$^\circ$.
Using the tangent ratio:
$\tan (\angle CPB) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{BC}{PB}$
Substitute the values:
$\tan 60^\circ = \frac{h + 1.6}{x}$
... (iii)
We know $\tan 60^\circ = \sqrt{3}$. Substitute $x=h$ from equation (ii) into equation (iii):
$\sqrt{3} = \frac{h + 1.6}{h}$
Multiply both sides by $h$:
$h\sqrt{3} = h + 1.6$
Rearrange the terms to isolate $h$:
$h\sqrt{3} - h = 1.6$
Factor out $h$:
$h(\sqrt{3} - 1) = 1.6$
Solve for $h$:
$h = \frac{1.6}{\sqrt{3} - 1}$
Rationalize the denominator by multiplying the numerator and denominator by $(\sqrt{3} + 1)$:
$h = \frac{1.6}{\sqrt{3} - 1} \times \frac{\sqrt{3} + 1}{\sqrt{3} + 1}$
$h = \frac{1.6(\sqrt{3} + 1)}{(\sqrt{3})^2 - (1)^2}$
$h = \frac{1.6(\sqrt{3} + 1)}{3 - 1}$
$h = \frac{1.6(\sqrt{3} + 1)}{2}$
$h = 0.8(\sqrt{3} + 1)$ m
... (iv)
Thus, the height of the pedestal is $0.8(\sqrt{3} + 1)$ meters.
Question 9. The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Answer:
Given:
Let AB be the building and CD be the tower.
A is the top and B is the foot of the building. C is the top and D is the foot of the tower.
Height of the tower, CD = 50 m.
The angle of elevation of the top of the building (A) from the foot of the tower (D) is $\angle$ADB = 30$^\circ$.
The angle of elevation of the top of the tower (C) from the foot of the building (B) is $\angle$CBD = 60$^\circ$.
The building and the tower are vertical, so $\angle$ABD = 90$^\circ$ and $\angle$CDB = 90$^\circ$.
Let the height of the building be AB = $h$ m.
Let the distance between the foot of the building and the foot of the tower be BD = $x$ m.
To Find:
The height of the building, $h$ (AB).
Solution:
Consider the right-angled triangle $\triangle$ABD.
In $\triangle$ABD, we have AB = $h$, BD = $x$, and $\angle$ADB = 30$^\circ$.
Using the tangent ratio:
$\tan (\angle ADB) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{AB}{BD}$
Substitute the values:
$\tan 30^\circ = \frac{h}{x}$
... (i)
We know $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
$\frac{1}{\sqrt{3}} = \frac{h}{x}$
Solving for $x$ in terms of $h$:
$x = h\sqrt{3}$ m
... (ii)
Now, consider the right-angled triangle $\triangle$CDB.
In $\triangle$CDB, we have CD = 50 m, BD = $x$, and $\angle$CBD = 60$^\circ$.
Using the tangent ratio:
$\tan (\angle CBD) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{CD}{BD}$
Substitute the values:
$\tan 60^\circ = \frac{50}{x}$
... (iii)
We know $\tan 60^\circ = \sqrt{3}$.
$\sqrt{3} = \frac{50}{x}$
Substitute the expression for $x$ from equation (ii) into this equation:
$\sqrt{3} = \frac{50}{h\sqrt{3}}$
Multiply both sides by $h\sqrt{3}$:
$\sqrt{3} \times h\sqrt{3} = 50$
$3h = 50$
Solve for $h$:
$h = \frac{50}{3}$ m
... (iv)
Thus, the height of the building is $\frac{50}{3}$ meters.
Question 10. Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
Answer:
Given:
Let AB and CD be the two poles of equal height, standing on either side of the road BD.
AB = CD = $h$ m.
Width of the road, BD = 80 m.
Let P be a point between the poles on the road.
The angle of elevation of the top of pole AB from P is $\angle$APB = 60$^\circ$.
The angle of elevation of the top of pole CD from P is $\angle$CPD = 30$^\circ$.
The poles are vertical, so $\angle$ABP = 90$^\circ$ and $\angle$CDP = 90$^\circ$.
Let the distance of point P from pole AB be BP = $x$ m.
Since P is on the road BD, the distance of point P from pole CD is PD = BD - BP = (80 - $x$) m.
To Find:
The height of the poles, $h$, and the distances of the point P from the poles (BP and PD).
Solution:
Consider the right-angled triangle $\triangle$ABP.
In $\triangle$ABP, we have AB = $h$, BP = $x$, and $\angle$APB = 60$^\circ$.
Using the tangent ratio:
$\tan (\angle APB) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{AB}{BP}$
Substitute the values:
$\tan 60^\circ = \frac{h}{x}$
... (i)
We know $\tan 60^\circ = \sqrt{3}$.
$\sqrt{3} = \frac{h}{x}$
Express $h$ in terms of $x$:
$h = x\sqrt{3}$ m
... (ii)
Now, consider the right-angled triangle $\triangle$CDP.
In $\triangle$CDP, we have CD = $h$, PD = $80 - x$, and $\angle$CPD = 30$^\circ$.
Using the tangent ratio:
$\tan (\angle CPD) = \frac{\text{Opposite side}}{\text{Adjacent side}} = \frac{CD}{PD}$
Substitute the values:
$\tan 30^\circ = \frac{h}{80 - x}$
... (iii)
We know $\tan 30^\circ = \frac{1}{\sqrt{3}}$.
$\frac{1}{\sqrt{3}} = \frac{h}{80 - x}$
Cross-multiply:
$80 - x = h\sqrt{3}$
... (iv)
Substitute the expression for $h$ from equation (ii) into equation (iv):
$80 - x = (x\sqrt{3})\sqrt{3}$
$80 - x = 3x$
Rearrange the terms to solve for $x$:
$80 = 3x + x$
$80 = 4x$
$x = \frac{80}{4}$
$x = 20$ m
... (v)
So, the distance of point P from pole AB is BP = 20 m.
The distance of point P from pole CD is PD = $80 - x = 80 - 20 = 60$ m.
Now, find the height of the poles $h$ using equation (ii):
$h = x\sqrt{3}$
Substitute $x=20$ from equation (v):
$h = 20\sqrt{3}$ m
... (vi)
The height of the poles is $20\sqrt{3}$ meters.
The distances of the point P from the poles are 20 m and 60 m.
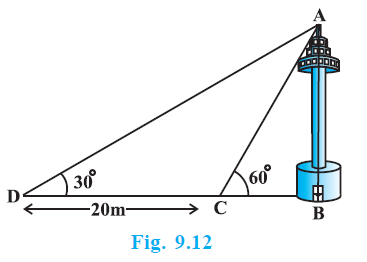
Question 11. A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joing this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig. 9.12). Find the height of the tower and the width of the canal.
Answer:
Given:
Let AB be the TV tower, where A is the top and B is the foot on one bank of the canal.
Let C be a point on the opposite bank directly opposite the tower.
The width of the canal is BC.
The angle of elevation of the top of the tower (A) from point C is $\angle$ACB = 60$^\circ$.
Let D be a point 20 m away from C on the line joining C to the foot of the tower (B). So, CD = 20 m.
The angle of elevation of the top of the tower (A) from point D is $\angle$ADB = 30$^\circ$.
The tower is vertical, so $\angle$ABC = 90$^\circ$.
Let the height of the tower be AB = $h$ m.
Let the width of the canal be BC = $x$ m.
The distance BD = BC + CD = $x + 20$ m.
To Find:
The height of the tower, $h$, and the width of the canal, $x$.
Solution:
Consider the right-angled triangle $\triangle$ABC.
Using the tangent ratio:
$\tan (\angle ACB) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 60^\circ = \frac{AB}{BC}$
Substitute the values:
$\sqrt{3} = \frac{h}{x}$
... (i)
From equation (i), we can express $h$ in terms of $x$:
$h = x\sqrt{3}$
... (ii)
Now, consider the right-angled triangle $\triangle$ABD.
Using the tangent ratio:
$\tan (\angle ADB) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 30^\circ = \frac{AB}{BD}$
Substitute the values:
$\frac{1}{\sqrt{3}} = \frac{h}{x + 20}$
... (iii)
Substitute the expression for $h$ from equation (ii) into equation (iii):
$\frac{1}{\sqrt{3}} = \frac{x\sqrt{3}}{x + 20}$
Cross-multiply:
$1 \times (x + 20) = \sqrt{3} \times x\sqrt{3}$
$x + 20 = 3x$
Rearrange the terms to solve for $x$:
$20 = 3x - x$
$20 = 2x$
$x = \frac{20}{2}$
$x = 10$ m
... (iv)
So, the width of the canal is 10 meters.
Now, find the height of the tower $h$ using equation (ii):
$h = x\sqrt{3}$
Substitute the value of $x$ from equation (iv):
$h = 10\sqrt{3}$ m
... (v)
The height of the tower is $10\sqrt{3}$ meters.
Thus, the height of the tower is $10\sqrt{3}$ meters and the width of the canal is 10 meters.
Question 12. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Answer:
Given:
Let AB be the building, where A is the top and B is the foot. AB = 7 m.
Let CD be the cable tower, where C is the top and D is the foot.
From the top of the building A, draw a horizontal line AE parallel to the ground BD, such that E is on CD.
The angle of elevation of the top of the cable tower (C) from A is $\angle$CAE = 60$^\circ$.
The angle of depression of the foot of the cable tower (D) from A is $\angle$EAD = 45$^\circ$.
Since AE || BD, the alternate interior angle $\angle$ADB = $\angle$EAD.
$\angle$ADB = 45$^\circ$
(Alternate interior angles)
The building is vertical, so $\angle$ABD = 90$^\circ$. The tower is vertical, so $\angle$CDB = 90$^\circ$ and $\angle$AEC = 90$^\circ$.
ABDE forms a rectangle, so AE = BD and ED = AB = 7 m.
Let the height of the cable tower be CD. CD = CE + ED = CE + 7.
To Find:
The height of the cable tower, CD.
Solution:
Consider the right-angled triangle $\triangle$ABD.
Using the tangent ratio in $\triangle$ABD:
$\tan (\angle ADB) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 45^\circ = \frac{AB}{BD}$
Substitute the values:
$1 = \frac{7}{BD}$
... (i)
Solving for BD:
$BD = 7$ m
... (ii)
Since AE = BD, we have AE = 7 m.
Now, consider the right-angled triangle $\triangle$AEC.
Using the tangent ratio in $\triangle$AEC:
$\tan (\angle CAE) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 60^\circ = \frac{CE}{AE}$
Substitute the values:
$\sqrt{3} = \frac{CE}{7}$
... (iii)
Solving for CE:
$CE = 7\sqrt{3}$ m
... (iv)
The height of the cable tower is CD = CE + ED.
Substitute the values of CE from equation (iv) and ED = 7 m:
$CD = 7\sqrt{3} + 7$
Factor out 7:
$CD = 7(\sqrt{3} + 1)$ m
... (v)
Thus, the height of the cable tower is $7(\sqrt{3} + 1)$ meters.
Question 13. As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Answer:
Given:
Let AB be the lighthouse, where A is the top and B is the base at sea-level. AB = 75 m.
Let the two ships be at points C and D on the sea-level, such that they are on the same side of the lighthouse and one is exactly behind the other. Assume D is further away from the lighthouse than C.
From the top of the lighthouse A, draw a horizontal line AX parallel to the sea-level BD.
The angle of depression of the ship at C from A is $\angle$XAC = 45$^\circ$. Since AX || BD, the alternate interior angle $\angle$ACB = $\angle$XAC.
$\angle$ACB = 45$^\circ$
(Alternate interior angles)
The angle of depression of the ship at D from A is $\angle$XAD = 30$^\circ$. Since AX || BD, the alternate interior angle $\angle$ADB = $\angle$XAD.
$\angle$ADB = 30$^\circ$
(Alternate interior angles)
The lighthouse is vertical to the sea-level, so $\angle$ABD = 90$^\circ$.
Let the distance of the nearer ship from the base of the lighthouse be BC = $x$ m.
Let the distance of the further ship from the base of the lighthouse be BD = $y$ m.
The distance between the two ships is CD = BD - BC = $y - x$ m.
To Find:
The distance between the two ships, CD.
Solution:
Consider the right-angled triangle $\triangle$ABC.
Using the tangent ratio:
$\tan (\angle ACB) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 45^\circ = \frac{AB}{BC}$
Substitute the values:
$1 = \frac{75}{x}$
... (i)
Solving for $x$:
$x = 75$ m
... (ii)
Now, consider the right-angled triangle $\triangle$ABD.
Using the tangent ratio:
$\tan (\angle ADB) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 30^\circ = \frac{AB}{BD}$
Substitute the values:
$\frac{1}{\sqrt{3}} = \frac{75}{y}$
... (iii)
Cross-multiply to solve for $y$:
$y = 75\sqrt{3}$ m
... (iv)
The distance between the two ships is CD = $y - x$.
Substitute the values from equations (ii) and (iv):
$CD = 75\sqrt{3} - 75$
Factor out 75:
$CD = 75(\sqrt{3} - 1)$ m
... (v)
Thus, the distance between the two ships is $75(\sqrt{3} - 1)$ meters.
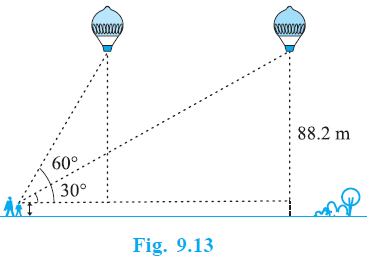
Question 14. A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval.
Answer:
Given:
Height of the girl = 1.2 m.
Height of the balloon from the ground = 88.2 m.
Let E be the eyes of the girl, located at a height of 1.2 m from the ground.
Draw a horizontal line EF from E, parallel to the ground.
Let the initial position of the balloon be A, and the final position be B.
Let P and Q be points on the horizontal line EF such that AP and BQ are perpendicular to EF.
The height of the balloon from the girl's eye level is AP = BQ = 88.2 m - 1.2 m = 87 m.
The initial angle of elevation of the balloon (A) from the girl's eyes (E) is $\angle$AEP = 60$^\circ$.
The final angle of elevation of the balloon (B) from the girl's eyes (E) is $\angle$BEQ = 30$^\circ$.
The distance travelled by the balloon is AB, which is equal to the distance PQ since the balloon moves horizontally.
To Find:
The distance travelled by the balloon, PQ.
Solution:
Consider the right-angled triangle $\triangle$AEP.
Using the tangent ratio:
$\tan (\angle AEP) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 60^\circ = \frac{AP}{EP}$
Substitute the values:
$\sqrt{3} = \frac{87}{EP}$
... (i)
Solving for EP:
$EP = \frac{87}{\sqrt{3}}$ m
... (ii)
Now, consider the right-angled triangle $\triangle$BEQ.
Using the tangent ratio:
$\tan (\angle BEQ) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 30^\circ = \frac{BQ}{EQ}$
Substitute the values:
$\frac{1}{\sqrt{3}} = \frac{87}{EQ}$
... (iii)
Solving for EQ:
$EQ = 87\sqrt{3}$ m
... (iv)
The distance travelled by the balloon is PQ = EQ - EP.
Substitute the values from equations (ii) and (iv):
$PQ = 87\sqrt{3} - \frac{87}{\sqrt{3}}$
Combine the terms:
$PQ = 87 \left(\sqrt{3} - \frac{1}{\sqrt{3}}\right)$
$PQ = 87 \left(\frac{3 - 1}{\sqrt{3}}\right)$
$PQ = 87 \left(\frac{2}{\sqrt{3}}\right)$
$PQ = \frac{174}{\sqrt{3}}$
Rationalize the denominator:
$PQ = \frac{174}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}$
$PQ = \frac{174\sqrt{3}}{3}$
$PQ = 58\sqrt{3}$ m
... (v)
Thus, the distance travelled by the balloon during the interval is $58\sqrt{3}$ meters.
Question 15. A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Answer:
Given:
Let AB be the tower, where A is the top and B is the foot on the highway. Let the height of the tower be AB = $h$ m.
Let C be the initial position of the car and D be the position of the car after 6 seconds. C, D, and B are points on the highway.
Let the observer be at A. Draw a horizontal line AX from A.
The initial angle of depression of the car at C is $\angle$XAC = 30$^\circ$.
The angle of depression of the car at D is $\angle$XAD = 60$^\circ$.
Since AX is horizontal and CB is the highway, AX || CB. Therefore, the alternate interior angles are equal:
$\angle$ACB = $\angle$XAC = 30$^\circ$
(Alternate interior angles)
$\angle$ADB = $\angle$XAD = 60$^\circ$
(Alternate interior angles)
The tower is vertical, so $\angle$ABC = 90$^\circ$.
Let the uniform speed of the car be $v$ m/s.
The distance covered by the car in 6 seconds is CD = $v \times 6 = 6v$ m.
Let the distance DB = $y$ m.
The distance CB = CD + DB = $6v + y$ m.
We need to find the time taken by the car to reach the foot of the tower from point D. Let this time be $t$ seconds. Then the distance DB = speed $\times$ time, so $y = v \times t$. We need to find $t$.
To Find:
The time taken by the car to reach the foot of the tower from point D.
Solution:
Consider the right-angled triangle $\triangle$ABD.
Using the tangent ratio:
$\tan (\angle ADB) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 60^\circ = \frac{AB}{DB}$
Substitute the values:
$\sqrt{3} = \frac{h}{y}$
... (i)
From equation (i), we can express $h$ in terms of $y$:
$h = y\sqrt{3}$ m
... (ii)
Now, consider the right-angled triangle $\triangle$ABC.
Using the tangent ratio:
$\tan (\angle ACB) = \frac{\text{Opposite side}}{\text{Adjacent side}}$
$\tan 30^\circ = \frac{AB}{CB}$
Substitute the values:
$\frac{1}{\sqrt{3}} = \frac{h}{6v + y}$
... (iii)
Substitute the expression for $h$ from equation (ii) into equation (iii):
$\frac{1}{\sqrt{3}} = \frac{y\sqrt{3}}{6v + y}$
Cross-multiply:
$1 \times (6v + y) = \sqrt{3} \times y\sqrt{3}$
$6v + y = 3y$
Rearrange the terms to solve for $y$:
$6v = 3y - y$
$6v = 2y$
$y = \frac{6v}{2}$
$y = 3v$ m
... (iv)
The time taken by the car to travel from D to B is the distance DB ($y$) divided by the speed ($v$).
Time taken $= \frac{y}{v}$
Substitute the value of $y$ from equation (iv):
Time taken $= \frac{3v}{v}$
Since $v \neq 0$ (the car is moving), we can cancel $v$:
Time taken $= 3$ seconds
... (v)
Thus, the time taken by the car to reach the foot of the tower from point D is 3 seconds.

